暗黙の前提を明らかにする「根拠と結論の図式化」とプロセスは次のとおりです。
- 意見を〈結論〉と〈根拠〉に分け、それぞれの間に「なぜならば」と「ゆえに」の矢印を引く
- 〈結論〉なぜならば⇒〈根拠〉というロジックはOKかチェックする
- 〈根拠〉ゆえに⇒〈結論〉というロジックはOKかチェックする
- 2と3のロジックが両方ともOKな場合「この意見は正当」と言える
- もし、3のロジック(上図の赤い矢印部分)が釈然としなければ、暗黙の前提を探す
- その暗黙の前提は正しいと言えるのか、根拠を考える
(『「自分で考える力」の授業』P.145より、一部編集のうえ抜粋)
「赤信号と横断歩道」の例でみてみましょう。結論と根拠の関係は次のとおりです。
| 結論 | 横断歩道を渡っちゃダメ! | |
|---|---|---|
| なぜならば↓ | ↑ゆえに | |
| 根拠 | 赤信号が点灯している | |
大人にとっては当たり前のことでも、子どもに説明すると「なんで赤信号だと渡っちゃダメなの?」と聞いてくることがあります。つまり、そこには子どもにとってはわからない「暗黙の前提」が隠れてるということです。これを丁寧に解きほぐしてみると
根拠:赤信号が点灯している
暗黙の前提:横断歩道が赤信号のときは、車用の信号は青なので危ない
結論:横断歩道を渡っちゃダメ!
という暗黙の前提がみつかりました。これと同様にして元の英語教材の例を考えると、提案者の視点では次のようなロジックになっています。
結論:この商品企画を進めるべき
根拠1:この商品はロングヒットが見込める
根拠2:内容がよければ10年以上売れる教材も多い
この場合は根拠は2段階なので、「結論と根拠1」「根拠1と根拠2(この場合、根拠1が結論の役割を担う)」で検討していきます。「結論と根拠1」についてはどちらの矢印についてもロジックが成り立ちそうですが、問題はその次です。
「内容がよければ10年以上売れる教材も多い。ゆえに、この商品はロングヒットが見込める」が本当に成立するのか疑問に思う人もいるでしょう。つまり、そこに「何らかの暗黙の前提がある」ということなので、考えをより深めるためには提案者に質問して明らかにする必要があるとわかります。
数字を使ってロジカルに考える
事業目的は各社で違えど、企業として存続するには利益を得ていかなければなりません。そのため、仕事では「利益率は何%になるのか」「シェアを何割奪う必要があるのか」などと、何事においても数字を使って考える必要があります。
とはいえ、会社における数字の使い方は学校の数学と異なり、計算して答えを出すのが目的ではありません。「数字から何を読み取り、どのような結論や推測が成り立つかを考える」ことが目的となるので、技術職を除けば+-×÷の四則演算ができればそれで事足りることがほとんどです。
むしろ問題となるのは、何かを読み取るにあたっての「数字のとらえ方」です。たとえば「受験者の半数を合格とするテストを実施したとき、平均点を取らなければ絶対に合格できない。〇か×か」という問いに対して、あなたはどう考えるでしょうか。
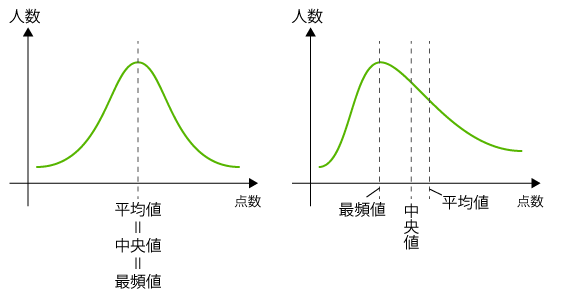
これは図にするとわかります。下図の左側のように50点くらいを中心として左右に同じように人数が分布しているならば平均値がそのまま中央値となります。そのため、平均点をとれれば合格できます。
しかし、「低得点者数<高得点者数、全体としては30点前後の受験者が最多」といった場合は、図の右側のように分布のピークが左側に偏るため「平均値≠中央値」となるので、平均点未満でも合格する可能性があります(逆に分布のピークが右側に偏れば、平均点をとっても不合格になりうる)。そのため、先の問いの「平均点を取らなければ絶対に合格できない。〇か×か」の答えは×となります。
ネットでよく見る「20代の平均貯蓄額は意外に高い400万円だった!」みたいな記事も、これと同様の理屈ですね。全体としては100万円未満の人数が多くても、成功した起業家やトレーダーなど一部のお金持ちが平均を引き上げるから意外に高い数字になる、というカラクリです。