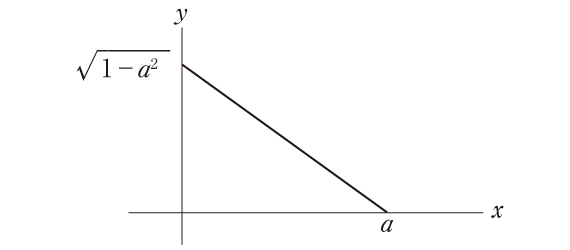A.4 円の中の2点の距離
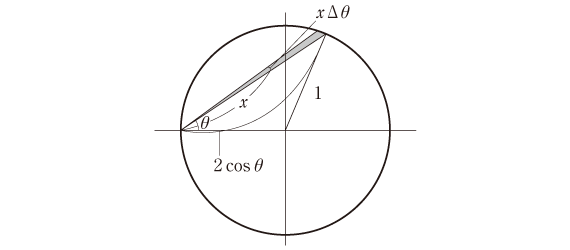
まず、円周上の点Aと円内の任意の点Bとの距離の期待値を求めます。この値は、Aを点(-1,0)に固定し、Bを円(原点中心、半径1)の上半分の中で動かして得られます。
先に答えの分子部分を計算します(それを分母部分の値――円の上半分の面積――で割った値が答えです[『数学<超絶>難問』Q40参照]。
まずθ、Δθを固定して、
\(\large{\int_{0}^{2\cos\theta}x\cdot x\Delta\theta dx=\Delta\theta\left[\frac{1}{3}x^3\right]^{2\cos\theta}_0=\frac{8}{3}(\cos^3\theta)\Delta\theta}\)
θは0から\(\large{\frac{\pi}{2}}$まで変わるので、
\(\large{\int_{0}^{\frac{\pi}{2}}\frac{8}{3}\cos^3\theta d\theta=\frac{8}{3}\int_{0}^{\frac{\pi}{2}}(1-\sin^2\theta)\cos\theta d\theta}\)
t=sinθとおくと、dt=cosθdθで、θが0→\(\large{\frac{\pi}{2}}\)、tが0→1で、
\(=\large{\frac{8}{3}\int_{0}^{1}(1-t^2)dt=\frac{16}{9}}\)
これを円の上半分の面積\(\large{\frac{\pi}{2}}\)で割って、答えは\(\large{\frac{32}{9\pi}}\)
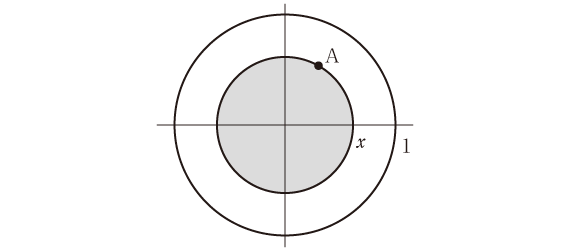
さて、円内の2つの点のうち、原点からより遠いほうをA、近いほうをBとよびます(たとえば出題ページの線分の長さはB―A で1回計算すればいいのであって、A―B で重ねて計算する必要はありません。したがって遠いほうをAとよぶ方法でいいのです)。
Aが半径xの円上を動くとき、その円内(上図のアミカケ部内)にあるBとAとの距離の期待値は\(\large{\frac{32x}{9\pi}}\)
したがって、答えは\(\large{\int_{0}^{1}2\pi x\cdot \pi x^2\cdot \frac{32x}{9\pi}dx\div\int_{0}^{1}2\pi x\cdot \pi x^2dx}\) ……(注)
=\(\large{\frac{128}{45\pi}}\)
(注)この式の意味はわかりにくいかもしれませんので、ちょっと補足説明をしておきましょう。この積分中の2πxは、Aが動く半径xの円のドット数のようなものであり、πx2は、Bが動く円内のドット数のようなものであり、それらをかけ合わせると、線分AB の総本数のようなものになるのです。これで感覚的にわかりますか?
A.5 壁に立てた棒の包絡線
上図のように、棒の端が(a,0)にあるとき、棒の方程式は、
\(\large{y=-\frac{\sqrt{1-a^2}}{a}x+\sqrt{1-a^2}}\) ……(1)
この棒と「端がa+Δaにあるときの棒」との交点が、Δa→0で包絡線上の点となります。この交点は、xを固定するとき、aの値が変わってもyの値が変わらないので、\(\large{\frac{dy}{da}=0}\)でなければなりません。
ゆえに\(\large{\frac{dy}{da}=\frac{x-a^3}{a^2\sqrt{1-a^2}}=0} ∴\large{a=x^\frac{1}{3}}\)
この値を(1)に代入して、\(\large{y=(1-x^{\frac{2}{3}})^{\frac{3}{2}} ∴x^{\frac{2}{3}}+y^{\frac{2}{3}}=1}\)
(ちなみに、この曲線はアストロイド(astroid)です)