Q.4 円の中の2点の距離
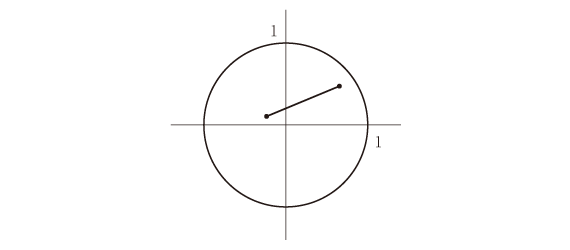
前回の記事では、円周上にある2点間の距離の期待値を求めました(リンク先Q.1参照)。今回は半径1の円の中に2つの点をランダムにおきます。2点間の距離の期待値は?
★「乱数を多量に発生させて、この期待値(平均値)の近似値を実験的に求めると、約0.9054となる」ことはよく知られているようです。本問では解析的に解いて、正確な値を求めてみましょう。
Q.5 壁に立てた棒の包絡線
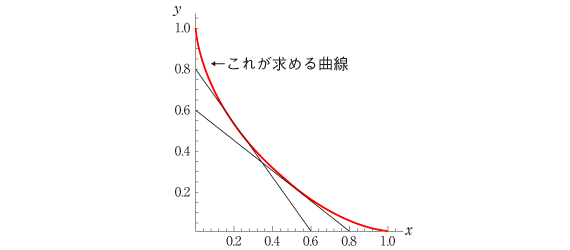
長さ1の棒が垂直な壁を下図のように滑っています。これから得られる包絡線(棒が通る領域と、棒が通らない領域との境界線)の方程式は?
ここから解答
A.1 3種のカードをそろえる(一般解問題)
1つ目がAだった場合、その後に買う箱数の期待値をEとすると、
- 次のカードがAなら、その1枚のほかにさらにE枚買わねばならず、
- 次のカードがBなら、さらにその後Cが出るまでの箱数期待値は\(\large{\frac{1}{c}}\)(注)
- 次のカードがCなら、さらにその後Bが出るまでの箱数期待値は\(\large{\frac{1}{b}}\)
したがって、\(E=a(1+E)+b(1+\frac{1}{c})+c(1+\frac{1}{b})\)
∴\(E=\large{\frac{1+\frac{c}{b}+\frac{b}{c}}{1-a}}\)……①
1つ目がBだった場合、同様に、\(E=\large{\frac{1+\frac{c}{a}+\frac{a}{c}}{1-b}}\)……②
1つ目がCだった場合、同様に、\(E=\large{\frac{1+\frac{b}{a}+\frac{a}{b}}{1-c}}\)……③
したがって求める答えは、
a(1+①)+b(1+②)+c(1+③)
=\(\large{1+\frac{a}{1-a}(1+\frac{c}{b}+\frac{b}{c})+\frac{b}{1-b}(1+\frac{c}{a}+\frac{a}{c})+\frac{c}{1-c}(1+\frac{b}{a}+\frac{a}{b})}\)
=\(\large{1+\frac{1}{a}+\frac{1}{b}+\frac{1}{c}-\frac{1}{1-a}-\frac{1}{1-b}-\frac{1}{1-c}}\)
(注)ある事象が、1回の試行で確率pで起こる場合、その事象が起こるまでの試行回数の期待値は\(\large{\frac{1}{p}}\)です。
《補足説明:期待値をEとおく。試行1回目で、pの確率でその事象が起こり、そのときはその1回で終了。一方、試行1回目で、(1−p)の確率でその事象は起こらず、そのときは、その1回に加えてさらにE回が必要。ゆえに、E=p×1+(1−p)(1+E) ∴E=\(\large{\frac{1}{p}}\)》