以前、『古典数学の難問101』『数学<超絶>難問』(いずれも小野田博一著、弊社刊)より、高校レベルから超難問まで10問を選りすぐり、数学マニア向けの挑戦状として掲載しました。
そして今回『数学<超・超絶>難問』を新たに発刊。同書から、さらに難しい問題を5問ピックアップしました。手ごたえのある問題を求める数学マニアの方は、ぜひ挑戦してみてください。
※本記事は「1ページ目~2ページ目前半:問題/2ページ目後半~4ページ:解答」の構成になっています。
※Smartnewsなどのアプリ内ブラウザでは数式が正常に表示されない場合があります。その際は、FirefoxやGoogle Chromeなど、単体のブラウザでお読みください。
ウォーミングアップ
Q1. 3種のカードをそろえる(一般解問題)
ある菓子の箱に、おまけとしてカードが必ず1枚入っています。カードにはAとBとCの3種類があり、Aが入っている確率はa、Bが入っている確率はb、Cが入っている確率はcです(a≠0、b≠0、c≠0、a+b+c=1)。その3種がそろうまでその菓子を買い続けるとします。あなたが買う菓子の個数の期待値は?
ここからが本番、超絶難問!
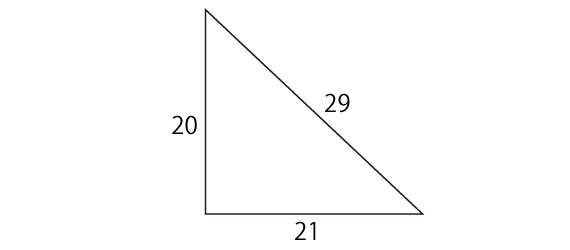
Q.2 直角をはさむ2辺の長さの差が1の「ピュタゴラス三角形」
3辺がどれも整数の直角三角形(ピュタゴラス三角形)のうち、直角をはさむ2辺の長さの差が1であるものについての問題です。斜辺の長さがもっとも短いのは、3-4-5の三角形で、2番目に短いのは、20-21-29の三角形です。さて、この三角形のうちで、斜辺の長さが6番目に短いものは?
Q.3 \({\Large{\frac{1}{2}!}}\)
ウォリス(JohnWallis、1616−1703)は\({\large{\frac{1}{2}!}}\)の値を求めました。そのために彼が何を使ったかを、ヒントとして下に書きます。完全に自力で解きたい人はその部分を見ないように注意してください。さて、あなたは\({\large{\frac{1}{2}!}}\)の値を求めることができますか?
★ヒントを見ずに本問を解いたら、あなたはまぎれもなく天才中の天才。ヒントを見たとしても、解けたならあなたはやはり天才でしょう(し、自分の才能にほれぼれとするでしょう)。
※ヒント:ウォリスが使ったのは\({\large{\int_{0}^{1}(x-x^2)^ndx}}\)です。