<解答編>幾何(難易度:超絶難問)
A7. アルキメデスの正七角形の作図・その1
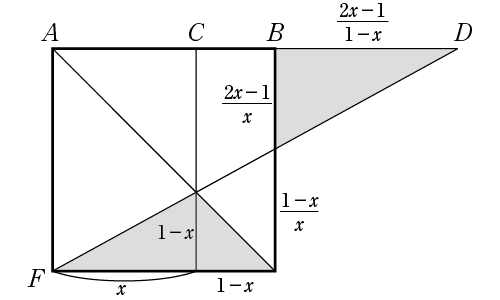
値を順に書き込んでいくと、下図のようになります。
網掛け部分の面積が等しいので、
\({\large \frac{1}{2}}(1-x)={\large \frac{1}{2}・\frac{2x-1}{1-x}・\frac{2x-1}{x}}\)
\(x(1-x)^2=(2x-1)^2\)
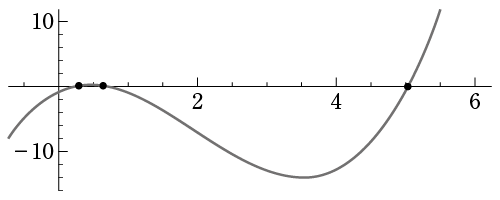
\(x^3-6x^2+5x-1=0\) …これが答え
この根3つのうち、求める値は\({\large \frac{1}{2}}<x<1\)のもので、近似値は約0.6431(厳密解はとても複雑な形になります)。
なお、他の根の近似値は約0.308と約5.05です。
A8. アルキメデスの正七角形の作図・その2
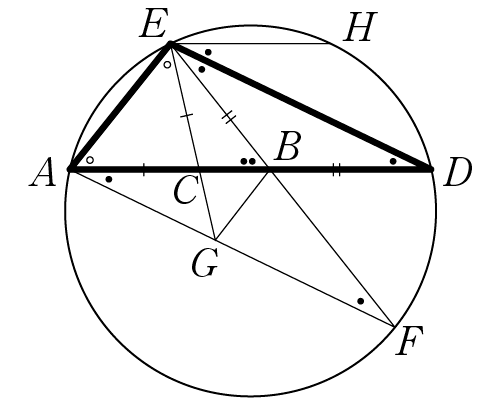
△AEDの外接円を描きます。EBを延長して、円との交点をFとします。ECを延長してAFとの交点をGとします。ADと平行にEから線を引き、円との交点をHとします。∠DEFの角度を●、∠AECの角度を○と表わすと、いろいろな角度が以下のように書き込めます。
CD・CB=AC2より\(\frac{CD}{AC}=\frac{AC}{CB}\)
AC=ECより\(\frac{CD}{EC}=\frac{EC}{CB}\)
ゆえに、△BCEと△ECDは相似で∠CEB=●
∠GAB=∠GEB なので四角形AEBGは円に内接します。ゆえに∠AEG=∠ABG=○
弦AGの円周角ABGと弦EBの円周角BAEが等しいので、AG=EB
AB・AC=BD2なので、\(\frac{AB}{BD}=\frac{BD}{AC}\)
BD=EB=AG,AC=ECなので、\(\frac{AB}{AG}=\frac{EB}{EC}\)
ゆえに△GABと△CEBは相似。したがって、○=●●
△AEDの内角の和は○○●●●、つまり●7つなので、●=\(\frac{180°}{7}\)
∠AEH=○●●●=●5つ=180°×\(\frac{5}{7}\)
これは確かに正七角形の内角の値です。