Q9. ディオパントスの問題(1)(解答:6ページ)
※以下の問題の答えは無数にあります。そのうちの1つを求めればOKです。なお、ディオパントスの問題における「平方数」とは、有理数の2乗の値である数のことです。たとえば、\((\frac{11}{17})^2\)は平方数で、\((\sqrt{6})^2\)は平方数ではありません。
\(ab+12,bc+12,ac+12\)のそれぞれが平方数であるような相異なる数\(a,b,c\)を求めよ。
(『算術』巻3,問題10)
[ヒント:\({\large \frac{1}{4}}+12={\large \frac{49}{4}}={\large (\frac{7}{2})^2}\)]
Q10. ディオパントスの問題(2)(解答:6ページ)
※Q9と同様に答えは無数にありますが、そのうちの1つを求めればOKです。
等比数列をなす3つの数のそれぞれから12を引いたものが、どれも平方数になるようにせよ。
《表現を変えると以下のとおり》
\(a-12,ab-12,ab^2-12\)がそれぞれ平方数となるような\(a,b\)を求めよ。
(『算術』巻5、問題1)
<解答編>ウォーミングアップ・幾何
A1. 円上の2点
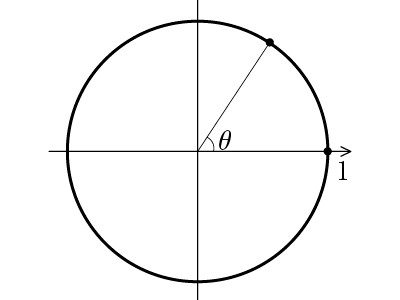
1つの点を(1,0)に固定し、もう1点を下図のように0≦θ≦πで動かして2点間の距離の平均値をとれば、それが答え。
2点間の距離(正の値)は
\(\begin{align*}\sqrt{(1-\cos\theta)^2+\sin^2\theta}&=\sqrt{2-2\cos\theta}\\&=\sqrt{4\sin^2\frac{\theta}{2}}\\&=2\sin\frac{\theta}{2}\end{align*}\)
したがって答えは、
\(\begin{align*}\frac{1}{\pi}\int_{0}^{\pi}2\sin\frac{\theta}{2}d\theta&=\frac{1}{\pi} \left[-4\cos\frac{\theta}{2}\right]^\pi_0\\&=\frac{4}{\pi}\end{align*}\)
A2. 半円と長方形
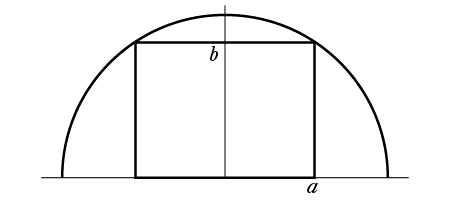
下図(\(a>0,b>0,a2+b2=1\))より、長方形の面積は、\(2ab=2\sqrt{a^2b^2}\)
相加相乗平均の関係より
\(2\sqrt{a^2b^2} ≦ 2×{\large \frac{a^2+b^2}{2}}=1\)
(等号が成り立つのは\(a=b=\frac{1}{\sqrt{2}}\)のとき)
つまり、1辺が\({\large \frac{1}{\sqrt{2}}}\)の正方形を左右に2つ並べた形のとき。