ウォーミングアップ・代数(難易度:高校生レベル)
Q4. 紀元前17世紀のパピルスの問題(解答:4ページ)
\({\huge \frac{2}{65}=\frac{1}{□}+\frac{1}{□}}\)
この□の中に入る、相違なる正の整数は?(答えは1つ示せばOK)
Q5. ピュタゴラス学派の平均値(紀元前6世紀)(解答:4ページ)
ピュタゴラス学派は少なくとも10種類の平均値を定義しました。そのうちの3つが、
- 相加(算術)平均:Arithmetic mean(以下ではA)
- 相乗(幾何)平均:Geometric mean(以下ではG)
- 調和平均:Harmonic mean(以下ではH)
で、定義は以下のとおりです(\(a,b\)はどちらも正の数)。
\(A={\Large \frac{1}{2}}(a+b)\)
\(G=\sqrt{ab}\)
\(H={\Large \frac{2ab}{a+b}}\)
\(a≠b\)のときH<G<Aが成り立ちます。あなたはこれを証明できますか?
(なお、\(a=b\)のとき、この3つの値は同じです)
Q6. 破産問題・一般解(勝負の条件が公平の時)(解答:4ページ)
AとBの2人がいて、2人の所持金はAがm円、Bがn円です。この2人がゲームを一方が破産するまで永久に続けます。ゲームは公平で、毎ゲームどちらが勝つ確率も\({\large \frac{1}{2}}\)です。勝者は敗者から1円巻き上げ(受け取り)ます。どちらかの所持金がなくなったら、対戦は終了です。
さて、AとBの勝率の比は?
幾何(難易度:超絶難問)
Q7. アルキメデスの正七角形の作図・その1(解答:5ページ)
アルキメデスは正七角形の作図方法を示しました。その方法に進む前に、準備用の問題をおきます。
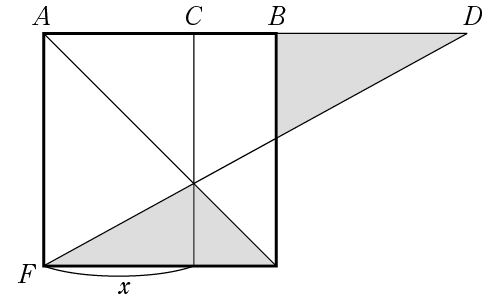
下図のように、単位正方形の頂点Fから直線FDを引いて、正方形の中のアミカケ部分と外のアミカケ部分の面積が等しくなるようにします。このときxは、どんな3次方程式をみたしますか?
Q8. アルキメデスの正七角形の作図・その2(解答:5ページ)
前問を解く過程で、AB・AC=BD2がみたされることがわかります。
また、CD・CB=AC2もみたされることがわかります(まだQ7に手を付けていない方は、せっかくですからチャレンジしてみてください)。
さて、これを使ってアルキメデスは、正七角形の作図方法を以下のように示しました。
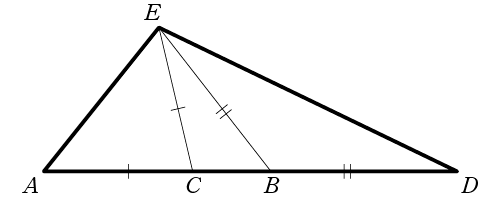
4点ACBDの位置はそのままで、下図のように点EをEC=ACとなるように、かつ、EB=BDとなるようにとります。するとAEは、「△AEDに外接する円」に内接する正七角形の1辺です。
あなたはこれを証明できますか?