web上には「数学知識や数学的思考を問う問題を紹介した記事」がたくさんありますが、タイトルに「東大生の正答率が数%」などとついてる割には論理よりひらめきが要求される問題だった、なんてことも少なくありません。数学好きの中には「もっと本格的な数学難問はないのか」と不満を募らせる人もいることでしょう。
そこで今回は『古典数学の難問101』『数学<超絶>難問』(いずれも小野田博一著、弊社刊)から、数学の問題をレベル別に厳選。ウォーミングアップとしての高校生向け問題から、ヌルさを排除した超難問まで計10問用意しました。
一目見て降参するもよし、解けるまで何日間も挑み続けるもよし。頭を悩ます問題をお楽しみください(なお、より難しい問題を集めた続編記事もあります。あわせてどうぞ!)
※本記事は「1~3ページ目前半:問題/3ページ後半~6ページ:解答」の構成になっています。※Smartnewsなどのアプリ内ブラウザでは数式が正常に表示されない場合があります。その際は、FirefoxやGoogle Chromeなど、単体のブラウザでお読みください。
ウォーミングアップ・幾何(難易度:高校生レベル)
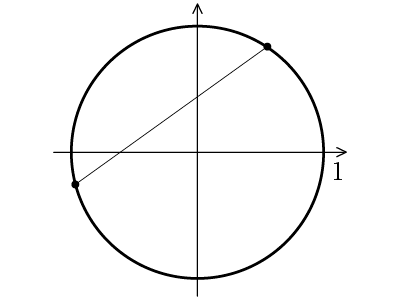
Q1. 円上の2点(解答:3ページ)
半径1の円周上にランダムに2点を置きます。その2点間の直線距離の期待値はいくらになりますか?
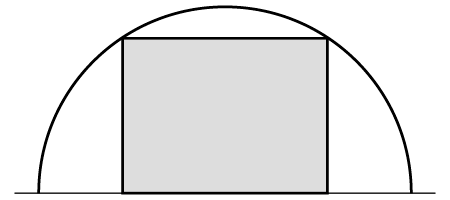
Q2. 半円と長方形(解答:3ページ)
半径1の半円があります。下図のように、長方形を、1辺は弦の上として半円に内接させる場合、長方形の面積が最大となるのはどんな長方形のとき?
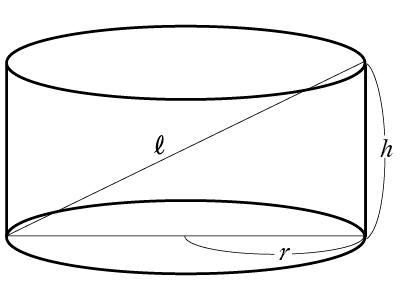
Q3. ケプラーのワイン樽の問題(解答:4ページ)
直立した円柱形をしたワイン樽について、その対角線の長さ\(l\)が決まっているとき、容積を最大にするためにはどうしたらよいでしょうか?